1+1は( )
息子「お父さん、おにぎりが1つあって、もう1つあるでしょ」
自分「うん」
息子「そして、それを混ぜて合わせたら、そのおにぎりは、2つでしょ」
自分「……いや、1つだよ」
息子「なんで?だってそのおにぎりは、1つのおにぎりより大きいよ」
自分「確かにそうだけど……でも、K(息子の名前)よりお父さんは体重が2倍以上あるけど、お父さんは二人じゃないよ」
息子「ああ、そうか!」
ある日、小学生の息子とそんなやりとりがあった。
「じゃあ、1たす1は2じゃないってことだね」と息子。
どう答えたらいいのか一瞬戸惑い、ふと思いついて「たとえば1かける1は1だよ」と伝えてみた。
すると、「1かける1の1は、おにぎりの1個とはちがう意味だから、これはかけ算じゃないよ」と、返ってきた。
数と係数の差異を、息子がぼんやり感知していることに驚いた
足し算でありながら、1+1が1になる。
その事実を、どう説明すればよいのか。
自分の数学的な素養では、彼の問いに納得できる説明を与えることができなかった。
息子は別の部屋にいた妻のところにもこの問いを持ち込み、妻はなぜか分数を持ち出してなんとか式を与えようとしたようだが、やはり納得には至らなかったらしい。
しばらくして、また息子がやってきた。
「1+1は2、じゃないことがあるね。この1は数じゃないからね」と言う。彼なりの理解が進んだようだが、私自身がこの件の把握に目下取り組み中にて追いつかない。
自分に数学的な素養はない。
だから、その1を重さとして捉え直すくらいしか、式にできる方法が思いつかない。
けれど、思いついたそれも自分の中では確信にはならなかった。
結果として、その「数ではない1」という謎は、息子に謎としてほのめかせるように誤魔化し、一旦そのまま放置することにした。
「事物としてのひとかたまり」と「整数としての1」。
その違いを、おにぎりという「混ぜ合わせられる事物」を通して、彼は肌で感じ取ったのかもしれない。
そう思いながら、むしろ自分のほうが困惑しはじめた。
閑話休題:
正方形がある。
この形態をFとする。その形態をその形態たらしめる内的条件をGとする。
端的にいえば、その正方形は、Gという内的条件によってFという形態を保っている。
この状態を、数学者ルネ・トムは擬群GFと呼ぶ。
彼によれば「ある種の形態は個別の価値をもち、ある種にとって重要性をもつことは生物学的に明らか」であり、さらに「その擬群GFがなんであるかを正確に定義することは一般的に困難、または不可能」とまで言っている。
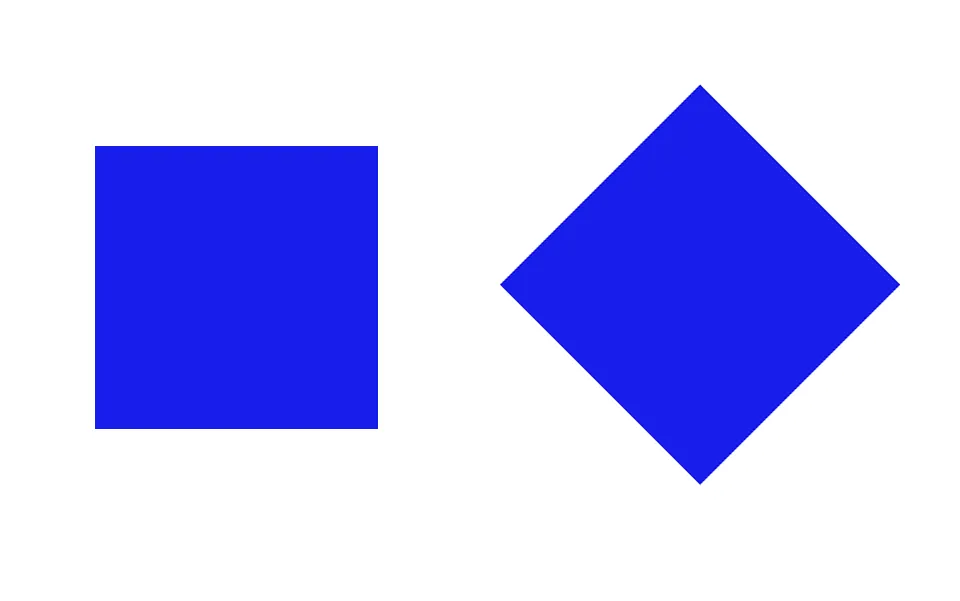
たとえば、上の図の2つの正方形は、どちらも同じGFをもっている。
しかし、右側は外的条件が異なり(45度傾けられている)、いわゆる「菱形」と呼ばれることになる。
つまり、両者は同じGF(としての1)でありながら、観察者の立場や配置条件の違いによって別の形態として知覚される。
この違いを数学的に厳密に区別しようとすると、思った以上に手間がかかる。……と、トムは言う。
どちらも、整数の1であり、ユークリッド的にはどちらも正方形なのだが、それでも、違う1なのだ。
また息子が近づいてきて「1たす1は、“おおきい1”、だと思う」
しばし呼吸をおき、「これは算数ではできない新しい答えだよ!だれも気づいてないかもしれない」と興奮のしきりである。一方未だに困惑したままの自分は「そうかもしれない、今度図書館で調べてみたら」と(内心ほうほうの体で)息子に伝えた。
彼がいつかこれに納得できる式を与えられるのか、明日にはまったく興味を失ってしまうのかわからないが、大人になってからでもふとこの問題を思い出すといいと思った。このおにぎりの1個をグラムに変換したり、米粒に分解したりして式を与えるのもわるくない。あるいは、ホカホカしてる1なのか、冷めてる1なのか、無限の変数が与えられるのだ。